The Importance Of Processes In Providing Services Shows The Overlap Between What Two Fields?
Abstract
A cycle is the simplest structure that brings redundant paths in network connectivity and feedback furnishings in network dynamics. An in-depth agreement of which cycles are of import and what role they play on network structure and dynamics, all the same, is still lacking. In this paper, we define the wheel number matrix, a matrix enclosing the information about cycles in a network, and the cycle ratio, an index that quantifies node importance. Experiments on real networks suggest that bike ratio contains rich information in improver to well-known criterion indices. For example, node rankings by bicycle ratio are largely unlike from rankings by degree, H-index, and coreness, which are very similar indices. Numerical experiments on identifying vital nodes for network connectivity and synchronization and maximizing the early reach of spreading show that the cycle ratio performs overall better than other benchmarks. Finally, we highlight a significant difference between the distribution of shorter cycles in existent and model networks. We believe our in-depth analyses on bike structure may yield insights, metrics, models, and algorithms for network science.
Introduction
The last two decades accept witnessed all-encompassing development in network scientific discipline (NS)1, with research focuses being shifted from discovering macroscopic properties2,iii,four to uncovering the functional roles played by microscopic structures, or fifty-fifty individual nodes and links5,6,7. Scientists take pieced an increasingly articulate picture about the functions of specific structures in disparate dynamical processes, such as the roles of unlike motifs in biological and communication networks5, how information and behaviors propagate along a contacting chainviii, and how a local star structure cocky-sustains an epidemic spreading procedureix,10.
Besides extensively studied chain and star structures, bike is another ubiquitously observed structure11, which plays significant roles in both structural organization and functional implementation. A cycle, likewise chosen loop in literature, can exist simply defined equally a closed path with the same starting and ending node. Recent studies take uncovered the topological backdrop of cycles, including the distribution of cycles of dissimilar sizes in real and artificial networks12,13,14,15,sixteen, the effect of degree correlations on the loops of calibration-free networks17, too as the significant roles of the cycles in network functions related to storage18, synchronizability19, and controllability20. Cycles are likewise used as a tool to measure out the extent of network being shut to tree networks, and thus a meaning divergence between model networks and real networks is found, that is, the quondam can't accurately reproduce the cycle structure in the latter21. In addition, the organization of cycles can be utilized to narrate private nodes and links. For example, a measure chosen clustering coefficient (likewise called local clustering coefficient)2 is based on counting the number of associated triangles (triangle is the cycle with smallest size), which recently considered the associated cycles with larger sizesxi,22,23, and was extended to the higher order cases22 and the weighted cases24,25. The edge multiplicity measures the number of triangles passing through an edge26. The issue of the addition of a none-observed link on the local organization of cycles tin exist used to estimate the likelihood of the existence of this link27, and the probability a self-avert random walker returns to the target node through a cycle (cycles with unlike lengths are assigned to different weights) can exist used to quantify the importance of the target node28.
Considering a elementary network where management and weight of a link are ignored and self-loops are not allowed, so a bicycle is the simplest construction providing redundant paths to all involved node pairs. That is to say, if ii nodes belong to a cycle, there are at least 2 independent paths connecting them. Such redundancy likewise brings complicated feedbacks in interacting dynamics. Therefore, the in-depth agreement of bike construction may provide insights and methods on how to maintain the network connectivity under attacks29, how to regulate interacting dynamics toward predesigned states30 and how to maximize the early on accomplish of spreading in brusk time31.
In this paper, according to the cycle-based statistics, we suggest a matrix (named cycle number matrix) to stand for bike information of network, and an index (named cycle ratio) to quantify the importance of individual nodes. This index is substantially unlike from well-known indices and methods7, producing a much different ranking of nodes comparing with degree3, H-index32, and corenessten. Extensive experiments on real networks in identifying the about vulnerable nodes under intentional attacks33,34, the well-nigh efficient nodes in pinning control35,36,37 and the nigh influential nodes in the early stage of epidemic spreading31,38 show that cycle ratio performs overall better than other benchmarks including degree, H-index, and coreness. Finally, we highlight a significant departure betwixt the distribution of shorter cycles in existent and model networks.
Results
Definition of bicycle ratio
Considering a simple network \(G(V,Due east)\), where Five and Due east are the sets of nodes and links, respectively. The size of a cycle equals the number of links it contains. The cycles containing node i with the smallest size are divers as node i's associated shortest cycles (as well called i's shortest cycles for simplicity) and the corresponding size is called node i's girthnineteen. Announce by \(S_i\) the set of the shortest cycles associated with node i, and \({{{{{Southward}}}}} = \cup _{{{{{{i}}}}} \in Five}S_{i}\) the ready of all shortest cycles of One thousand, we ascertain the and so-called cycle number matrix \(C = \left[ {c_{ij}} \right]_{Northward \times Northward}\) to characterize the bike structure of G, where N=|Five| is the number of nodes in G, and \(c_{ij}\) is the number of cycles in S that laissez passer through both nodes i and j if \(i \ne j\). If \(i = j\), \(c_{ii}\) is the number of cycles in Due south that incorporate node i. Apparently, \(C\) is a symmetric matrix. Based on the bicycle number matrix, we advise an index, named bicycle ratio, to measure a node's importance every bit
$$r_i = \left\{ {\begin{assortment}{*{twenty}{c}} {0,c_{ii} = 0} \\ {\mathop {\sum}\nolimits_{j,c_{ij} \, > \, 0} {\frac{{c_{ij}}}{{c_{jj}}},c_{ii} \, > \,0.} } \end{array}} \right.$$
(ane)
According to the above definition, if a node i doesn't vest to any bicycle in South, its cycle ratio is reasonably prepare to be zero. When \(c_{ii} > 0\), all items in the summation are well defined since \(c_{jj} > 0\) if \(c_{ij} > 0\). The ratio estimates the importance of node i subject to its participation to other nodes' shortest cycles in S. Note that, in our definition, just shortest cycles associated with each node are considered since cycles with larger sizes are unremarkably less relevant to the network functions (we have also tested on longer cycles, see details in Discussion) and to account for all cycles is infeasible for most networks due to the tremendous computational complexity27 (Supplementary Fig. 1 in Supplementary Notation 1 shows the number of cycles with different lengths, indicating an exponential growth). Figure 1a presents an case network, and Fig. 1b shows the corresponding cycle number matrix. The process to calculate the cycle ratio of an example node (i.east., node 1) is also shown in Fig. 1b. In Eq. 1, each term represents the degree to which node i (i=1 for this example) participates in \(j\)'s associated shortest cycles (\(j = 1,2,iii,4\,{{{{{{{\mathrm{and}}}}}}}}\,5\) for this example) in which denominator is the number of shortest cycles of node \(j\), and the numerator is the number of cycles associated with both node i and node \(j\). For case, the second term in the example equation in Fig. 1b, 3/4, means that iii of the four shortest cycles of node 2 ({2, 3, ane}, {2, 4, one}, {2, 1, 5}, {2, four, 3}) incorporate node 1. In a word, \(r_1\) represents the degree to which node 1 participates in associated shortest cycles of other nodes. The cycle ratios of all nodes are presented in Fig. 1c. Three well-known node centralities, degreethree, H-index32, and coreness10 (meet precise definitions of these indices in Methods), are used as benchmarks for comparing. Their values for this example network are also presented in Fig. 1c.
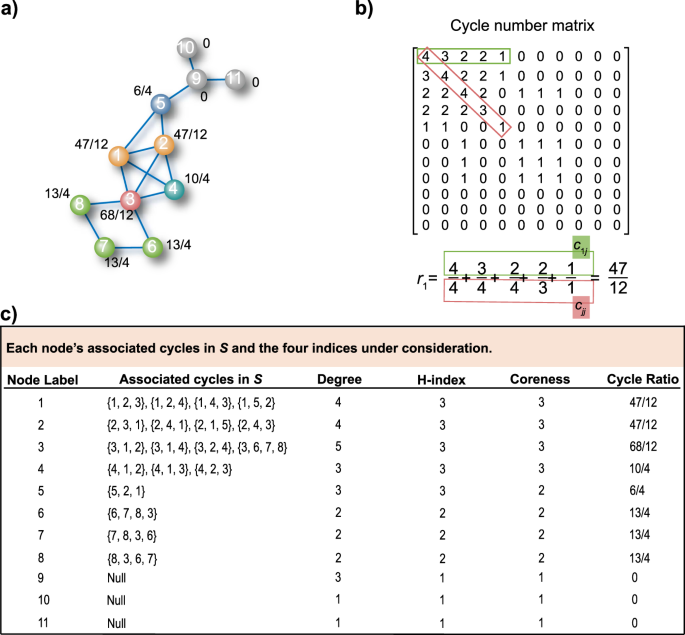
a An example network with cycle ratios of nodes. Here the number in each node is its label, the value next to it is its wheel ratio and nodes of the same color have the same cycle ratio. b The cycle number matrix of case network in (a) and how to calculate the cycle ratio of node i. Here the chemical element \(c_{ij}\) in cycle number matrix is the number of shortest cycles that laissez passer through both nodes \(i\) and \(j\) if \(i\, \ne\, j\). If \(i = j\), \(c_{2}\) is the number of shortest cycles that contain node \(i\). For node 1 the non-zero elements in the green square in the matrix are neighbors with mutual shortest cycles with node one, and each value (\(c_{1j}\), where \(j = one,2,3,4\,{{{{{{{\mathrm{and}}}}}}}}\,5\)) represents the number of these cycles. The elements in the red square (\(c_{jj}\), where \(j = 1,two,3,four\,{{{{{{{\mathrm{and}}}}}}}}\,five\)) are the number of shortest cycles of each neighbor. The sum of the ratios of \(c_{1j}\) and \(c_{jj}\) is the cycle ratio of node 1. c Every node's associated cycles in \(S\), degree, H-index, coreness10 and cycle ratio. Here \(S\) is the prepare of all shortest cycles of example network in (a) and \(South = \{ \{ 1,2,iii\} ,\{ i,2,4\} ,\{ ane,2,v\} ,\{ 1,3,four\} ,\{ ii,3,iv\} ,\{ 3,6,7,8\} \}\).
Information
Nosotros test the performance of cycle ratio in identifying vital nodes discipline to iii well-studied dynamical processes, node percolation33,34, synchronization30, and epidemic spreading38. The first one considers nodes' power to maintain the network connectivity, the 2d ane accounts for nodes' capacity to regulate interacting dynamics toward a certain predesigned state, and the last i concentrates on infected nodes' reach in the early stage of an epidemic outbreak. The experiments are carried out on six real networks from disparate fields, including the neural network of C. elegans (C. elegans)39, the e-mail advice network of the Academy at Rovira i Virgili in Espana (E-mail)twoscore, the collaboration network of jazz musicians (Jazz)41, the collaboration network of scientists working on NS42, the US air transportation network (USAir)32, and the protein-protein interaction network of yeast (Yeast)43. Their basic topological features are summarized in Table i.
Correlation analysis
Before penetrating into each index'southward power to identify vital nodes, we first meet whether bike ratio contains rich data in improver to the 3 benchmarks. Nosotros apply the Kendall's Tau (\(\tau\))44,45 to measure the correlation between pairs of indices (see the definition of \(\tau\) in Methods). Given 2 indices X and Y, if \(\tau (X,Y)\) is close to 1, it indicates that X and Y are highly correlated and less differential to each other. Figure 2 shows the average correlation matrix between all alphabetize pairs for the six networks (the correlation matrix for each network is shown in Supplementary Fig. ii in Supplementary Note 2), one can clearly observe that the correlations betwixt degree, H-index, and coreness are markedly high than the correlations betwixt bicycle ratio and the other three, the average of \(\tau\) over the vi networks is 0.89 for the former and 0.61 for the latter. That is to say, the resulted node rankings produced past degree, H-index, and coreness are very like to each other. Therefore, although the performance of H-alphabetize or coreness in some specific tasks is better than caste10,32, the node rankings produced by H-index and coreness contain less information in add-on to the i produced past degree, and vice versa. In contrast, as suggested by the lower correlations, the node rankings produced by cycle ratio take rich data in addition to these produced by caste, H-index, and coreness. This is a very important yet like shooting fish in a barrel-to-be-ignored marker nigh the potential value of the proposed alphabetize since the lower correlations between the proposed index and known indices bespeak a college possibility that the proposed alphabetize will provide insights beyond known indices. Besides, Supplementary Annotation iii shows the distributions of the four indices for the six real networks under consideration. Ane tin can observe that the distinguishability of cycle ratio with almost fractions is skillful while the distinguishability of coreness is poor.
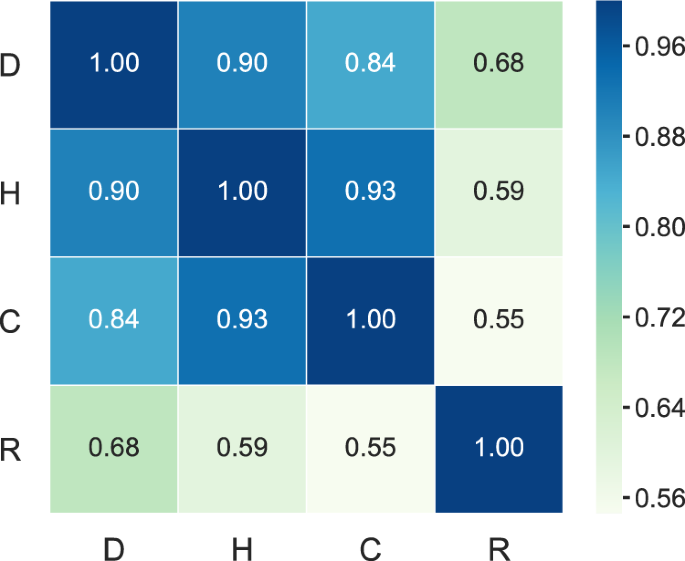
Here D, H, C and R represent degree, H-index, coreness, and cycle ratio, respectively. Details of the six networks are shown in Table 1. Each element is the averaged value of the correlation \(\tau\) betwixt the two indices corresponding to its position over the six networks, and the value is visualized past the color. See detailed calculation of the correlation \(\tau\) in Methods.
We are interested in comparing the difference between cycle ratio and local clustering coefficient which is the simplest alphabetize based on the neighborhood cycles. The local clustering coefficient of a node in network is the fraction of triangles that really exist over all possible triangles in its neighborhood. In despite of the conceptual overlap, cycle ratio is largely unlike from local clustering coefficient in three aspects: (i) the considered shortest cycles (i.east., cycles in \(S\)) are not necessarily to be triangles; (ii) bike ratio is non a local alphabetize since even node \(i\) and node j are distant in a network, the value of \(c_{ij}\) can be nonzero; (three) cycle ratio is not a ratio just the sum of ratios, and thus its value can be greater than 1. Supplementary Note four compares the difference between cycle ratio and clustering coefficient in particular and shows that the correlations between clustering coefficient and the other four indices are the everyman. Although clustering coefficient can reflect the local connexion, it cannot reverberate the importance of a node. Observe that, due to the sparsity and hierarchical organization of many real networks, the local clustering coefficient is usually negatively correlated with degree (typically, local clustering coefficient scales as \(k^{ - 1}\))46,47, and thus not a good index for influential nodes. Similarly, Supplementary Fig. 12 in Supplementary Note 5 shows that the correlations betwixt eigenvector axis48 and the other 4 indices are low.
Figure 3 presents visualized Yeast network respective to the resulted rankings past the 4 indices. Very intuitively, the vital nodes selected past degree, H-index, and coreness are densely connected with each other and amassed in a sure region, in consequent to the so-called rich-club miracle49,fifty. As a contrast, the vital nodes selected by cycle ratio are scattered in the whole network with sparser connections among them. This is a significant advantage of cycle ratio if i would like to detect out a set up of vital nodes, considering if the selected vital nodes tend to be amassed to each other, their influential areas will be highly overlapped and thus their collective influences are probably weaker10,51,52. Therefore, we believe the in-depth analyses of bicycle ratio may uncover insights that cannot be direct obtained by other benchmark centralities.
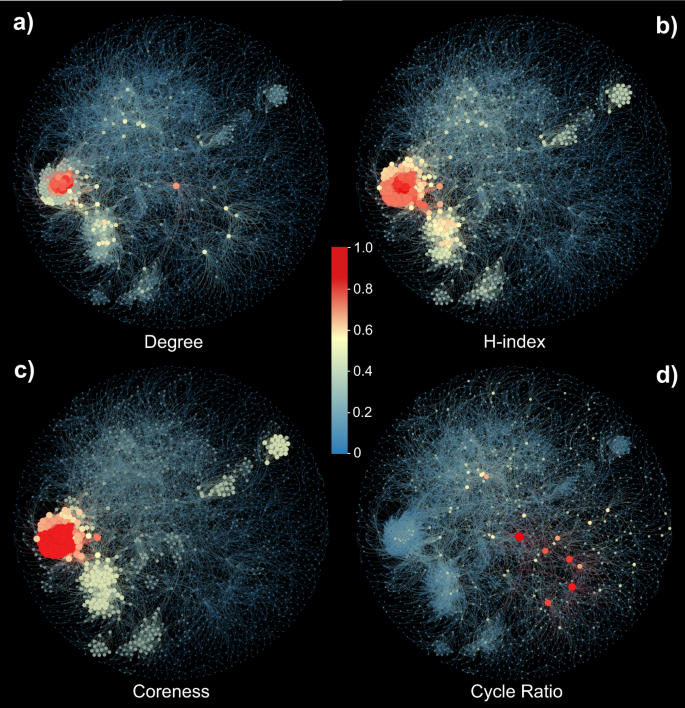
The Yeast network is taken for case. In each plot, the sizes and colors of nodes are proportional to their relative values of the respective indices normalized past their respective maximum values. The position of each node in the four plots is fixed. For instance, in (a), a node i'south relative value is \(k_i/k_{{{\mathrm{max}}}}\) where \(k_i\) is i's degree and \(k_{{{\mathrm{max}}}}\) is the maximum degree of Yeast. Analogously, (b– d) show the results of H-alphabetize, coreness and wheel ratio, respectively. In (a– c), the vital nodes are densely connected with each other and clustered in several certain regions, and this effect increases in turn. In (d), however, the state of affairs is completely dissimilar where the vital nodes scattered throughout the whole network.
Percolation
To evaluate the importance of nodes in maintaining the network connectivity, we study the node percolation dynamics33,34. Given a network, nosotros remove one node at each time step and calculate the size of the largest component of the remaining network until the remaining network is empty. The metric called Robustness53 is used to measure out the operation, defined every bit
$$R = \frac{ane}{N}\mathop {\sum}\nolimits_{n = 1}^N {g\left( n \right),}$$
(2)
where the relative size \(g(n)\) is the number of nodes in the largest component divided past N after removing n nodes. The normalization cistron 1/Due north ensures that the values of R of networks with different sizes can exist compared. For each alphabetize, we compute once to get a stock-still ranking of nodes. The node with largest alphabetize value is removed preferentially. Patently, a smaller R ways a quicker collapse and thus a ameliorate performance. Figure 4a shows the collapsing processes in the six real networks, resulted from the node removal by bicycle ratio and the other three indices. For the majority of the considered networks, bicycle ratio leads to much faster collapse than other indices. Figure 4b exhibits the Robustness R, from which one can see that the bike ratio is overall the best index in identifying the most vital nodes in maintaining the network connectivity. In improver, Supplementary Figs. 10 and 13 in Supplementary Annotation 4 and Supplementary Note 5 respectively show the results of clustering coefficient and eigenvector centrality, respectively, and the same conclusion can exist obtained.
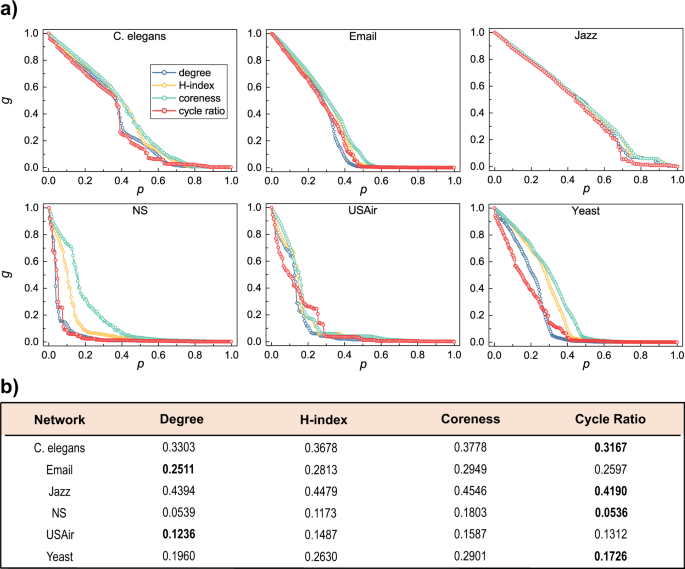
a The \(x\)-axis denotes the ratio of removed nodes and the \(y\)-axis shows the relative size of the largest component after node removal. For each index, the node with the largest index value is removed each time and calculate the size of the largest component of the remaining network. b The robustness \(R\) of the four indices for the six real networks. For each network, best performed index with minimum robustness \(R\) is emphasized in bold.
Pinning command
We side by side evaluate the importance of nodes by measuring the effect acquired by pinning these nodes in a synchronizing process35,36. Considering a general case where a simple connected network \(G\left( {V,E} \correct)\) is consisted of N linearly and diffusively coupled nodes, with an interacting dynamics as
$$\dot x_i = f( {x_i} ) + \sigma \mathop {\sum}\nolimits_{j = one}^North {l_{ij}{{\Gamma }}( {x_j} )} + U_i( {x_i, \ldots ,x_N} ),$$
(3)
where the vector \(x_i \in {{{{{{{\mathbf{R}}}}}}}}^n\) is the state of node i, the function \(f( \cdot )\) describes the self-dynamics of a node, the positive constant \(\sigma\) denotes the coupling forcefulness, U i is the controller applied at node i, and the inner coupling matrix \({{\Gamma }}:{{{{{{{\mathbf{R}}}}}}}}^n \to {{{{{{{\mathbf{R}}}}}}}}^n\) is positive semidefinite. The Laplacian matrix \(Fifty = [l_{ij}]_{N \times Due north}\) of G is defined as follows. If \((i,j) \in E\), and so \(l_{ij} = - one\); if \((i,j)\, \notin\, E\) and \(i\, \ne\, j\), then \(l_{ij} = 0\); if \(i = j\), then \(l_{2} = - \mathop {\sum}\nolimits_{j \ne 1} {l_{ij}}\). The goal of pinning control is to bulldoze the system from any initial country to the target land in finite time past pinning some selected nodes. Analogous to the node percolation, all nodes are ranked in the descending order by a given index. Then, we successively pin nodes ane past 1 co-ordinate to the ranking and quantify the synchronizability of the pinned networks, which can be measured by the reciprocal of the smallest nonzero eigenvalue of the principal submatrix54,55 (a smaller value corresponds to a higher synchronizability), namely \(1/\mu _1(L_{ - Q})\), where Q is the number of pinned nodes, \(L_{ - Q}\) is the principal submatrix, obtained by deleting the Q rows and columns corresponding to the Q pinned nodes from the original Laplacian matrix L, and \(\mu _1(L_{ - Q})\) is the smallest nonzero eigenvalue of \(L_{ - Q}\). Inspired by the metric Robustness, we propose a similar metric named pinning efficiency to characterize the operation of an index subject to pinning control, as
$$P = \frac{1}{{Q_{{{\mathrm{max}}}}}}\mathop {\sum}\nolimits_{Q = 1}^{Q_{{{\mathrm{max}}}}} {\frac{1}{{\mu _1(L_{ - Q})}}} ,$$
(4)
where \(Q_{{{\mathrm{max}}}}\) is the maximum number of pinned nodes under simulation. Here we fix \(Q_{{{\mathrm{max}}}} = 0.3N\), and we have checked that the choices of \(Q_{{{\mathrm{max}}}}\) will not affect the decision. Figure 5a shows how \(1/\mu _1(L_{ - Q})\) decays with increasing number of pinned nodes. Obviously, a faster decay corresponds to a improve performance. Figure 5b compares the pinning efficiency of the 4 indices. Similar to the upshot of the node percolation, cycle ratio is overall the best alphabetize in identifying the virtually efficient nodes in pinning control. In addition, Supplementary Tables 1 and 2 in Supplementary Note iv and Supplementary Note v respectively testify the results of clustering coefficient and eigenvector centrality and the aforementioned conclusion can be obtained.
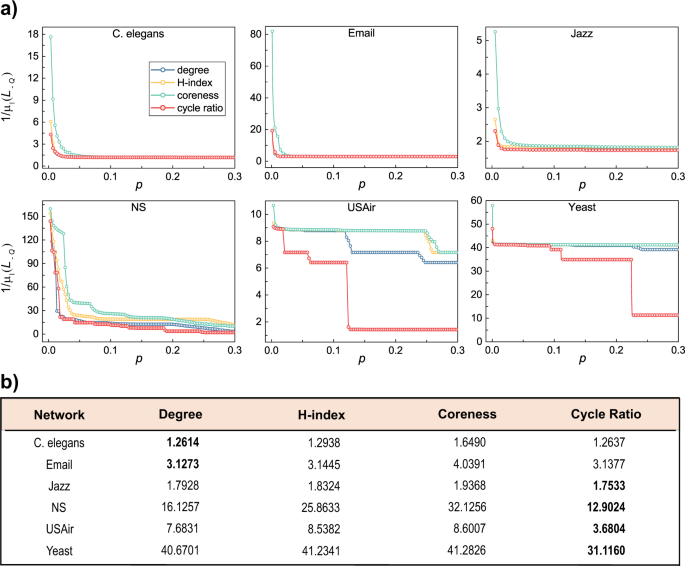
a The x-axis denotes the ratio of pinned nodes and the \(y\)-axis shows network synchronizability after pinning the fraction of nodes. For each index, the nodes are pinned i past i in descending social club of the index and quantify the synchronizability of the pinned networks each time. b The pinning efficiency \(P\) of the 4 indices for the six existent-globe networks. For each network, best performed index with minimum pinning efficiency \(P\) is emphasized in assuming.
Epidemic spreading
Lastly, nosotros consider the spreading dynamics. Since in viral marketing and online information transmission, people are more interested in maximizing the achieve in brusque time, and in epidemiological control, the most critical issue is the spreading range and control measures in the early stage of outbreak (e.g., see the discussion of the efficacy of early command measures for COVID-nineteen56,57, we concentrate on the fast influencers that play the dominant part in the early on phase31. To quantify the influence of a fix of selected nodes, nosotros simulate the standard susceptible-infected-recovered (SIR) spreading dynamics38, where at each time step, each susceptible node will be infected by an infected neighbor with probability \(\beta\), and each infected node volition exist recovered with probability \(\gamma\). Initially, the pinnacle-0.1N nodes selected by each index are set to be infected and others are susceptible. The indices are ranked by cumulative infected nodes at a certain time footstep t, the more the better. Nosotros consider the instance at \(\beta = \beta _c\) and \(\gamma = one\), where
$$\beta _c = \langle k \rangle /\left( {\langle k^ii \rangle - \langle g \rangle} \correct)$$
(five)
is the spreading threshold9,38 when \(\gamma = i\). Here \(\langle grand \rangle\) and \(\langle grand^2 \rangle\) are the average degree and the average squared degree, respectively. Figure 6 reports the rankings of the 4 indices at fourth dimension steps \(t = 1\), \(t = 2\), \(t = four\) and \(t = 8\), where the values are averaged over 2000 contained runs. The all-time-performed index is ranked No. i, the runner up is ranked No. 2, …, and the worst ane is ranked No. 4. Amidst the 24 matches (i.e., 6 networks and 4 time steps), cycle ratio gets ranked No. i for 23 times and No. 2 for ane time, information technology dramatically outperforms other indices. In addition, Supplementary Figs. 11 and xiv in Supplementary Annotation 4 and Supplementary Notation 5 respectively show the results of clustering coefficient and eigenvector centrality and the aforementioned conclusion can be obtained. The results for more \(\left( {\beta ,t} \right)\) parameter sets are presented in Supplementary Note 6. In fact, the spreading capacity of cycle ratio is superior to coreness for both unmarried-source and multiple-source cases, including fast spreading (considering the performance at the early stage) and complete spreading (see Supplementary Note vii).
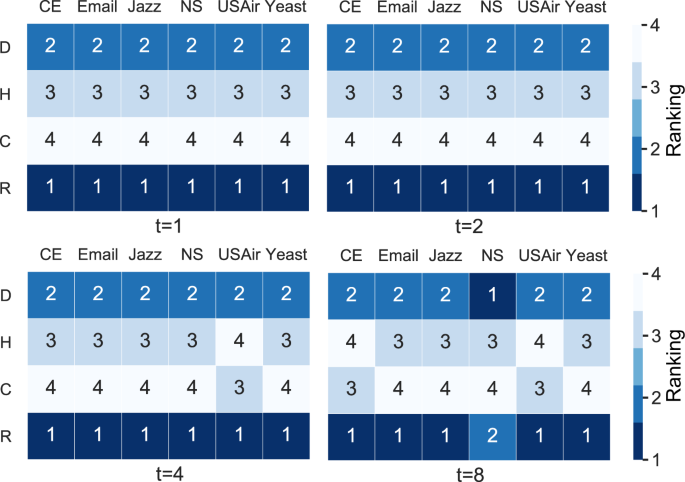
Each matrix presents the results of the comparison of the iv indices in a given time step of the spreading procedure. D, H, C and R correspond degree, H-index, coreness, and cycle ratio, respectively. CE is the abbreviation of C. elegans. The elements in each matrix are the rankings of 4 indices at the corresponding fourth dimension step, which is determined by cumulative infected nodes of each index in the SIR model simulation. The index with the largest number of infected nodes is ranked No. 1, and the others are ranked No. 2, 3, and iv successively. Each ranking is averaged over 2000 independent runs and they are visualized past the color: the better the deeper. The infection probability is set as β =β c. for each network.
In addition to real networks, we have too analyzed two types of synthetic networks, the Erdős–Rényi (ER) networks58 and Barabási–Albert (BA) networksthree. The overall performance of cycle ratio is simply in the center of the 4 indices. The reason for the not-and then-expert operation may exist that the random networks are less localized (as indicated by the very minor clustering coefficient) with lengths of shortest cycles (i.e., cycles in S) being relatively longer than existent networks with similar sizes and densities (see Supplementary Note 8 and Supplementary Note 9), and thus furnishings of cycles on dynamical processes are weaker6,59.
Discussion
To represent bicycle information of a network, this paper defines a matrix, called cycle number matrix, with which an alphabetize, called cycle ratio, tin can be calculated to quantify the importance of an individual node past simply measuring to which extent it is involved in other nodes' associated shortest cycles. The basic idea underlying such an index is that if cycles are of import in maintaining connectivity and interacting dynamics, so a node involved in many cycles should be vital. Experiments on real networks bear witness that cycle ratio outperforms the other indices in identifying vital nodes that are critical in maintaining the network connectivity, efficient in pinning control and influential in epidemic spreading. In node percolation, information technology should be noted that the performance will be affected by dynamics itself in the way of greedy removal, so the removal order here is stock-still as the effect of the first calculation. Our finding thus has potential applicability in practice. For the node percolation, the top-ranked nodes should be firstly protected to maintain the network connectivity if there is a risk of functional loss of nodes. Reversely, if one would similar to initiate an intentional attack, the top-ranked nodes are considered to be the primary targets. Such scenario is relevant to power grids60, air transportation networks, financial networks61, Internet, and so on62. Notation that, when we consider an attack to an airport in the modern order, it does not mean we demand to physically destroy it just disturb its data systems and signal systems. The critical nodes in pinning control can be pinned to efficiently approach the consensus of multiple agents63 and to ensure the coordination of unmanned aerial vehicles64 and mobile sensor networks65. Lastly, we proved bicycle ratio is an efficient alphabetize for finding the susceptible individuals that need to exist vaccinated in the early stage of epidemic spreading26,31.
It's worth noting that the operation of cycle ratio is not necessarily meliorate if longer cycles are considered. This is because when the longer cycles are counted, the difference in local cycle structure might be depressed. That is to say, the sets of associated cycles of many nodes volition get more like (i.east., with larger overlap), which may eventually atomic number 82 to the decrease of the discriminability and thus the accuracy of the cycle ratio (see Supplementary Annotation x).
An obvious insufficiency of wheel ratio is that it cannot be applied for trees or tree-similar networks. Even for normal networks, a fraction of nodes may be non associated with whatever cycles. These nodes' influences may be unlike but they are all assigned the same cycle ratio zero. I straightforward way to solve this issue is to combine cycle ratio with some other indices, for example, a mixed index could be \(r^ \ast = r_i + \varepsilon k_i\) with \(\varepsilon\) existence a tunable parameter, hence all nodes with nada cycle ratio tin can be ranked past their degrees. Since cycle ratio and degree will produce markedly dissimilar rankings, a subtly designed combination of cycle ratio and degree has the potential to generate much improve results than the single index. Similar improvement could also be achieved by combining cycle ratio with H-alphabetize or coreness. In contrast, the expected improvement by combining degree, H-index and coreness is lower since they are already very like to each other. We go out this detailed problem for future written report.
In addition, the method used to characterize the bicycle structure can be extended to deal with hypernetworks66, where a hyperedge represents the interaction between multiple nodes. Treating hyperedges as the cycles in the set S and denoting \(\Omega\) the incidence matrix, whose element \(\Omega _{ie}\) indicates whether node i belongs to hyperedge eastward (\(\Omega _{ie} = 1\) indicates the belongness and \(\Omega _{ie} = 0\) otherwise), so we tin obtain a matrix similar to the cycle number matrix by multiplying the incidence matrix by its transposed matrix, say \(\Omega \Omega ^T\), where the diagonal element [ΩΩ T ] ii represents the number of hyperedges involving node i and [ΩΩ T ] ij indicates the number of hyperedges that involving both node i and node j. Therefore, nosotros can quantify a node's importance in a hypernetwork by its participation to other nodes' hyperedges.
Nosotros end this newspaper by presenting two open problems. Firstly, analogous to bike ratio, one may also design cycle-based indices to quantify the likelihood of the existence of any unobserved link, which can find applications in solving the link prediction problem. Secondly, the good performance of cycle ratio, likewise as the lower correlations betwixt cycle ratio and other benchmark centralities, encourages the in-depth studies on cycle structure. In terms of global statistics, the model networks have lower average clustering coefficient and lower proximity to tree networks than existent networks21; in terms of the distribution of shorter cycles, as shown in Supplementary Note nine, none of degree-preserved nil model67, Watts–Strogatz model2 and Barabasi–Albert model3 tin can well reproduce the cycle-based statistics of real networks, indicating that the understanding about how cycles are formed may deepen our knowledge on the mechanisms underlying network organization. In improver to the shortest cycles, college-gild cycles also play of import roles in network structure and functions68,69. Thus nosotros expect to observe more insights from spectral analysis of the bike number matrix and analyzing longer and higher-order cycles in the future with the help of methodologies from algebraic topology69,lxx and sufficient computational resource, and extend the findings and telescopic of applications reported in this paper.
Methods
Caste, H-index and Coreness
Degree of a node is the number of its immediate neighbors. H-alphabetize of a node i is the maximum integer h such that at that place are at least h neighbors of node i with degrees no less than h. Coreness is obtained by the chiliad-core decompositionx. The yard-core decomposition process starts by removing all nodes with degree \(thousand = 1\). This may cause new nodes with caste \(1000 \le 1\) to appear. These are also removed and the procedure stops when all remaining nodes are of degree \(k\, > \,i\). The removed nodes and their associated links form the one-crush, and the nodes in the one-shell are assigned a coreness value 1. This pruning process is repeated to extract the two-shell, that is, in each step the nodes with degree \(1000 \le two\) are removed. Nodes in the ii-shell are assigned a coreness value 2. The process is continued until all higher-layer shells take been identified and all nodes have been removed. In the literature, coreness is likewise referred to as g-crush index10.
Kendall'southward Tau
We consider whatsoever two indices associated with all N nodes, \(Ten = (x_1,x_2, \ldots ,x_N)\) and \(Y = (y_1,y_2, \ldots ,y_N)\), too as the Northward two-tuples \(( {x_1,y_1} ),( {x_2,y_2} ), \ldots ,(x_N,y_N)\). Any pair \(( {x_i,y_i} )\) and \(( {x_j,y_j} )\) are concordant if the ranks for both elements agree, namely if both \(x_i \, > \,x_j\) and \(y_i > y_j\) or if both \(x_i < x_j\) and \(y_i < y_j\). They are discordant if \(x_i > x_j\) and \(y_i < y_j\) or if \(x_i < x_j\) and \(y_i > y_j\). Here \(n_ +\) and \(n_ -\) are used to stand for the number of concordant and discordant pairs, respectively. In improver, \(t_X\) is the number of the pairs in which \(x_i = x_j\) and \(y_i \ne y_j\), and \(t_Y\) is the number of the pairs in which \(x_i \, \ne \,x_j\) and \(y_i = y_j\). Notice that if \(x_i = x_j\) and \(y_i = y_j\), the pair is not added to either \(t_X\) or \(t_Y\). Comparison all \(North(Due north - 1)/2\) pairs of two-tuples, the Kendall's Tau is defined equally44
$$\tau = \frac{{\left( {n_ + - n_ - } \right)}}{{\sqrt {\left( {n_ + + n_ - + t_X} \right)} \times \sqrt {\left( {n_ + + n_ - + t_Y} \right)} }}.$$
(6)
If 10 and Y are contained, \(\tau\) should be shut to zero, and thus the extent to which τ exceeds nothing indicates the force of correlation. The above definition of Kendall's Tau44 is an improved version of the original definition45, specifically designed to deal with the case with many equivalent elements.
Data availability
The networks data that support the findings of this report are available through the respective references32,39,40,41,42,43 or at the following github repository: https://github.com/ftl129/CycleRatio.
Code availability
The custom code that supports the findings of this report is available at the following github repository: https://github.com/ftl129/CycleRatio.
References
-
Newman, M. E. J. Networks. Oxford Univ. Press (2018).
-
Watts, D. J. & Strogatz, S. H. Collective dynamics of 'minor-globe' networks. Nature 393, 440–442 (1998).
-
Barabási, A.-50. & Albert, R. Emergence of scaling in random networks. Sci. (80) 286, 509–512 (1999).
-
Newman, M. East. J. Assortative mixing in networks. Phys. Rev. Lett. 89, 208701 (2002).
-
Alon, U. Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450–461 (2007).
-
Lü, L. & Zhou, T. Link prediction in complex networks: a survey. Phys. A 390, 1151–1170 (2011).
-
Lü, L. et al. Vital nodes identification in circuitous networks. Phys. Rep. 650, 1–63 (2016).
-
Christakis, Northward. A. & Fowler, J. H. The spread of obesity in a big social network over 32 years. N. Engl. J. Med. 357, 370–379 (2007).
-
Castellano, C. & Pastor-Satorras, R. Thresholds for epidemic spreading in networks. Phys. Rev. Lett. 105, 218701 (2010).
-
Kitsak, Yard. et al. Identification of influential spreaders in complex networks. Nat. Phys. 6, 888–893 (2010).
-
Kim, H.-J. & Kim, J. M. Cyclic topology in complex networks. Phys. Rev. E 72, 036109 (2005).
-
Bianconi, G. & Capocci, A. Number of loops of size h in growing calibration-gratis networks. Phys. Rev. Lett. 90, 078701 (2003).
-
Bianconi, G., Caldarelli, G. & Capocci, A. Loops structure of the Internet at the autonomous organization level. Phys. Rev. Due east 71, 11–14 (2005).
-
Bianconi, G., Gulbahce, North. & Motter, A. Due east. Local structure of directed networks. Phys. Rev. Lett. 100, 118701 (2008).
-
Rozenfeld, H. D., Kirk, J. Due east., Bollt, E. M. & Ben-Avraham, D. Statistics of cycles: How loopy is your network? J. Phys. A. Math. Gen. 38, 4589–4595 (2005).
-
Bonneau, H., Hassid, A., Biham, O., Kühn, R. & Katzav, E. Distribution of shortest cycle lengths in random networks. Phys. Rev. East 96, 062307 (2017).
-
Bianconi, G. & Marsili, K. Issue of degree correlations on the loop structure of scale-complimentary networks. Phys. Rev. E 73, 066127 (2006).
-
Lizier, J. T., Atay, F. Grand. & Jost, J. Information storage, loop motifs, and amassed construction in circuitous networks. Phys. Rev. East 86, 026110 (2012).
-
Shi, D., Chen, G., Thong, W. W. One thousand. & Yan, X. Searching for optimal network topology with best possible synchronizability. IEEE Circuits Syst. Magazine. 13, 66–75 (2013).
-
Ruths, J. & Ruths, D. Control profiles of circuitous networks. Sci. (80) 343, 1373–1376 (2014).
-
Zhang, West., Li, West. & Deng, Due west. The characteristics of cycle-nodes-ratio and its application to network nomenclature. Commun. Nonlinear Sci. Numer. Simul. 99, 105804 (2021).
-
Fronczak, A., Hołst, J. A., Jedynak, M. & Sienkiewicz, J. Higher gild clustering coeffcients in Barabási-Albert networks. Phys. A 316, 688–694 (2002).
-
Caldarelli, Grand., Pastor-Satorras, R. & Vespignani, A. Structure of cycles and local ordering in complex networks. Eur. Phys. J. B 38, 183–186 (2004).
-
Barrat, A., Barthélemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. 101, 3747–3752 (2004).
-
Saramäki, J., Kivelä, K., Onnela, J. P., Kaski, 1000. & Kertész, J. Generalizations of the clustering coefficient to weighted complex networks. Phys. Rev. E 75, 2–five (2007).
-
Pei, S. & Makse, H. A. Spreading dynamics in complex networks. J. Stat. Mech. Theory Exp. 2013, P12002 (2013).
-
Pan, L., Zhou, T., Lü, L. & Hu, C. K. Predicting missing links and identifying spurious links via likelihood analysis. Sci. Rep. 6, 22955 (2016).
-
Van Kerrebroeck, V. & Marinari, E. Ranking vertices or edges of a network by loops: a new approach. Phys. Rev. Lett. 101, 1–4 (2008).
-
Albert, R., Jeong, H. & Barabási, A.-L. Error and assail tolerance of complex networks. Nature 406, 378–382 (2000).
-
Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y. & Zhou, C. Synchronization in complex networks. Phys. Rep. 469, 93–137 (2008).
-
Zhou, F., Lü, L. & Mariani, G. S. Fast influencers in circuitous networks. Commun. Nonlinear Sci. Numer. Simul. 74, 69–83 (2019).
-
Lü, L., Zhou, T., Zhang, Q. Grand. & Stanley, H. E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. seven, 10168 (2016).
-
Callaway, D. Due south., Newman, Thousand. E. J., Strogatz, South. H. & Watts, D. J. Network robustness and fragility: Percolation on random graphs. Phys. Rev. Lett. 85, 5468–5471 (2000).
-
Cohen, R., Erez, K., Ben-Avraham, D. & Havlin, S. Breakup of the net under intentional set on. Phys. Rev. Lett. 86, 3682–3685 (2001).
-
Wang, X. F. & Chen, G. Pinning control of scale-complimentary dynamical networks. Phys. A 310, 521–531 (2001).
-
Li, X., Wang, 10. & Chen, G. Pinning a complex dynamical network to its equilibrium. IEEE Trans. Circuits Syst. I 51, 2074–2087 (2004).
-
Qiu, Z., Fan, T., Li, M. & Lü, L. Identifying vital nodes past Achlioptas procedure. N. J. Phys. 23, 033036 (2021).
-
Pastor-Satorras, R., Castellano, C., Van Mieghem, P. & Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 87, 925–979 (2015).
-
Rossi, R. A. & Ahmed, North. K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Twenty-Ninth AAAI Conference on Artificial Intelligence 4292–4293 (AAAI Press, 2015).
-
Guimerà, R., Danon, 50., Díaz-Guilera, A., Giralt, F. & Arenas, A. Cocky-like community structure in a network of human being interactions. Phys. Rev. East 68, 065103 (2003).
-
Gleiser, P. M. & Danon, L. Customs construction in jazz. Adv. Circuitous Syst. 06, 565–573 (2003).
-
Newman, M. Eastward. J. Finding customs structure in networks using the eigenvectors of matrices. Phys. Rev. E 74, 036104 (2006).
-
Jeong, H., Bricklayer, Due south. P., Barabási, A. 50. & Oltvai, Z. N. Lethality and centrality in poly peptide networks. Nature 411, 41–42 (2001).
-
Knight, Westward. R. A computer method for computing Kendall'southward tau with ungrouped data. J. Am. Stat. Assoc. 61, 436–439 (1966).
-
Kendall, Chiliad. G. A new measure of rank correlation. Biometrika 30, 81–93 (1938).
-
Ravasz, E. & Barabási, A.-50. Hierarchical organization in circuitous networks. Phys. Rev. E 67, 026112 (2003).
-
Zhou, T., Yan, Thou. & Wang, B.-H. Maximal planar networks with large clustering coefficient and power-law degree distribution. Phys. Rev. E 71, 046141 (2005).
-
Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 2, 113–120 (1972).
-
Zhou, S. & Mondragón, R. J. The rich-social club phenomenon in the cyberspace topology. IEEE Commun. Lett. 8, 180–182 (2004).
-
Colizza, 5., Flammini, A., Serrano, K. A. & Vespignani, A. Detecting rich-gild ordering in complex networks. Nat. Phys. two, 110–115 (2006).
-
Zhang, J. X., Chen, D. B., Dong, Q. & Zhao, Z. D. Identifying a prepare of influential spreaders in complex networks. Sci. Rep. 6, 1–10 (2016).
-
Ji, S., Lü, L., Yeung, C. H. & Hu, Y. Effective spreading from multiple leaders identified by percolation in the susceptible-infected-recovered (SIR) model. North. J. Phys. nineteen, 073020 (2017).
-
Schneider, C. M., Moreira, A. A., Andrade, J. Southward., Havlin, Due south. & Herrmann, H. J. Mitigation of malicious attacks on networks. Proc. Natl Acad. Sci. 108, 3838–3841 (2011).
-
Liu, H., Xu, X., Lu, J. A., Chen, Thousand. & Zeng, Z. Optimizing pinning control of complex dynamical networks based on spectral properties of grounded Laplacian matrices. IEEE Trans. Syst. Man, Cybern. Syst. 51, 786–796 (2018).
-
Pirani, One thousand. & Sundaram, S. On the smallest eigenvalue of grounded Laplacian matrices. IEEE Trans. Autom. Contr. 61, 509–514 (2016).
-
Liu, Q.-H. et al. The COVID-19 outbreak in Sichuan, China: Epidemiology and impact of interventions. PLOS Comput. Biol. sixteen, e1008467 (2020).
-
Chen, D. & Zhou, T. Evaluating the effect of Chinese control measures on COVID-19 via temporal reproduction number estimation. PLoS 1 16, e0246715 (2021).
-
Erdős, P. & Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hungarian Acad. Sci. v, 17–60 (1960).
-
Katz, L. A new condition alphabetize derived from sociometric analysis. Psychometrika 18, 39–43 (1953).
-
Albert, R., Albert, I. & Nakarado, Chiliad. 50. Structural vulnerability of the North American power grid. Phys. Rev. Eastward 69, 025103 (2004).
-
Haldane, A. Grand. & May, R. M. Systemic take a chance in banking ecosystems. Nature 469, 351–355 (2011).
-
Li, M. et al. Percolation on complex networks: theory and application. Phys. Rep. 907, one–68 (2021).
-
Chen, F., Chen, Z., Xiang, L., Liu, Z. & Yuan, Z. Reaching a consensus via pinning command. Automatica 45, 1215–1220 (2009).
-
Tang, Y., Gao, H., Kurths, J. & Fang, J. A. Evolutionary pinning control and its awarding in UAV coordination. IEEE Trans. Ind. Inform. eight, 828–838 (2012).
-
Ögren, P., Fiorelli, Due east. & Leonard, N. East. Cooperative command of mobile sensor networks: adaptive gradient climbing in a distributed environs. IEEE Trans. Autom. Contr. 49, 1292–1302 (2004).
-
Suo, Q., Guo, J. L. & Shen, A. Z. Data spreading dynamics in hypernetworks. Phys. A Stat. Mech. its Appl 495, 475–487 (2018).
-
Maslov, Southward. & Sneppen, Thou. Specificity and stability in topology of protein networks. Sci. (80) 296, 910–913 (2002).
-
Sizemore, A. Eastward. et al. Cliques and cavities in the human being connectome. J. Comput. Neurosci. 44, 115–145 (2017).
-
Shi, D., Lü, L. & Chen, 1000. Totally homogeneous networks. Natl Sci. Rev. half dozen, 962–969 (2019).
-
Mahadevan, P., Krioukov, D., Fall, K. & Vahdat, A. Systematic topology analysis and generation using degree correlations. Comput. Commun. Rev. 36, 135–146 (2006).
Acknowledgements
This work is supported by the National Natural Scientific discipline Foundation of China (Nos. 11622538, 61673150, 61433014, 11975071), and the Zhejiang Provincial Natural Science Foundation of China (No. LR16A050001). L.L. and T.Z. acknowledges the Science Strength Promotion Programme of UESTC.
Author information
Affiliations
Contributions
T.F., L.L., and D.S. conceived the idea and designed the experiments and T.Z. provided a complement to the blueprint. T.F. and L.L. performed the research. All authors analyzed the data. T.F., Fifty.L., and T.Z. wrote the paper. D.S. edited this paper. All authors discussed the results and reviewed the paper.
Corresponding authors
Ideals declarations
Competing interests
The authors declare no competing interests.
Peer review data
Communications Physics thanks Yanqing Hu and the other, anonymous, reviewer(due south) for their contribution to the peer review of this piece of work.
Boosted data
Publisher's note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Admission This article is licensed under a Creative Commons Attribution four.0 International License, which permits utilize, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give advisable credit to the original author(south) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third political party textile in this article are included in the article'south Creative Commons license, unless indicated otherwise in a credit line to the fabric. If material is not included in the commodity's Creative Commons license and your intended use is not permitted past statutory regulation or exceeds the permitted use, you will need to obtain permission straight from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/four.0/.
Reprints and Permissions
Most this article
Cite this article
Fan, T., Lü, Fifty., Shi, D. et al. Characterizing bicycle construction in circuitous networks. Commun Phys four, 272 (2021). https://doi.org/10.1038/s42005-021-00781-three
-
Received:
-
Accepted:
-
Published:
-
DOI : https://doi.org/10.1038/s42005-021-00781-3
Further reading
Comments
Past submitting a annotate you concord to bide by our Terms and Community Guidelines. If yous find something abusive or that does not comply with our terms or guidelines please flag it every bit inappropriate.
The Importance Of Processes In Providing Services Shows The Overlap Between What Two Fields?,
Source: https://www.nature.com/articles/s42005-021-00781-3
Posted by: edgertonwasmand.blogspot.com


0 Response to "The Importance Of Processes In Providing Services Shows The Overlap Between What Two Fields?"
Post a Comment